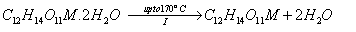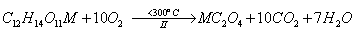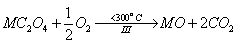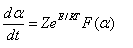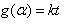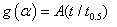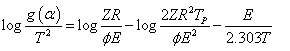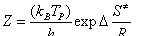Past Issues
Degradation Kinetics of Some Coordination Biopolymers of Transition Metal Complexes of Alginates: Influence of Geometrical Structure and Strength of Chelation on the Thermal Stability
Refat M Hassan1*, Hideo D Takagi2
1Department of Chemistry, Faculty of Science, Assiut University, Assiut, Egypt 2Chemistry Department, School of Science, Research Center of Materials Science, Nagoya, Japan
*Corresponding author: Refat M Hassan, Department of Chemistry, Faculty of Science, Assiut University, Assiut 71516 Egypt.
Received: November 21, 2019 Published: December 18, 2019
ABSTRACT
Non isothermal (TG) and (DTG) thermal techniques have been applied for studying degradation kinetics of some coordination biopolymers of transition metal complexes such as Mn(II)-, Co(II)-, Ni(II)-, Cu(II)- and Zn(II)-metal-ions coordinated with the carboxylate and hydroxyl functional groups of alginate as a natural polymer. Three stages of degradation for such complexes have been observed. The first one was corresponding to the dehydration of two coordinated water molecules, followed by degradation of the formed dehydrated derivatives in the two following stages, respectively. Metal oxalates were formed as intermediate fragments. Sets of different models applied to compute the kinetic parameters of degradation. The kinetic results of degradation revealed that the stability was increased in the order Zn < Mn ≤ Co < Ni < Cu–alginates. A tentative degradation mechanism in terms of the complexes thermal stability, model structure, geometrical configuration and strength of chelation is discussed.
Keywords: Degradation, Transition Metals, Complexes, Kinetics, Thermal Stability.
INTRODUCTION
Alginate polysaccharide is a natural polymer containing β (1-4) linked D-mannuronic acid units and some L-gulurounic acid units in a linear-block copolymer structure [1-5]. Alginate possesses a high affinity for chelating with silver (I) and polyvalent metal ions particularly with the divalent ions [6-8].
The crosslinks have been existed through formation of partially ionic and partially coordinate bonds between the chelated metal ion and both the carboxylate and hydroxyl groups, respectively, of the alginate macromolecular chains of the guluronic blocks in order to form its corresponding coordination biopolymer metal-alginate gel complexes [9,10].
Although, the recognized high importance of those polymeric biomaterials in biotechnological industry through numerous studies of its physicochemical properties [11-18], a little attention was paid to studies of degradation kinetics from the thermal stability points of view.
In terms of the arguments mentioned above and our interest on the thermal decomposition studies of such coordination biopolymer complexes metal-alginates [19-21], we have prompted to undertake the cited work in an effort to gain some information on the influence of the thermal stability of these complexes on the performance efficiency in terms of the model structure, coordination geometry and strength of chelation points of view. Again, the results obtained will be compared with that reported previously for other coordination biopolymers complexes of divalent-metal alginates [19-21].
EXPERIMENTAL
MATERIALS
All materials used were of Analar quality (BDH). Samples of granule nature of such metal alginate complexes were prepared by replacement of the sodium counter ions in alginate (Na+) (Cica Reagent Chemical Co.) by Mn2+, Co2+, Ni2+, Cu2+ and Zn2+ metal ions. The process takes place by stepwise addition of alginate powder to solutions of metal ion electrolytes placed in glass conical flasks (ca. 0.5-1.0 M) whilst stirring the solutions vigorously to avoid any gelatinous precipitate formation, which swells with difficulty. After completion of between the two exchangeable ions (2-3 hrs), the formed granules of metal alginates were washed with deionized water several times, and then with doubly distilled water until the resultant washings became free from the surrounding metal ions [20,21]. The sample complexes were dried at 105oC under vacuum over anhydrous CaCl2 or P2O5 [20,21].
TECHNIQUES
Thermogravimetry (TG) and differential thermogravimetry (DTG) of metal alginate complexes were carried out using a Mettler TA 3000 thermal analyzer in static air. Three degrees 5, 10 and 20 K/min of heating rates were used.
A Pye Unicam SP 3100 spectrophotometer using the KBr disc technique (4000~200 cm-1) was used to record the IR spectra.
A Philips 1710 diffractometer, the patterns run with copper as a target and nickel as a filter (λ = 1.54187 Å) at 40kV and 30 mA was applied to record the X-ray diffraction patterns. The scanning speed was 3.6 K/min in the range 2θ = 2-60.
RESULTS AND DISCUSSION
Generally, the divalent metal ions from the electrolytes were replaced the Na+ counter ions of added alginate powder through ion exchange process. This ion exchange is inherently a stoichiometric process [11-13], even the two counter ions may different in either valences or mobilities [6]. The exchange processes can be represented by the following stoichiometric equation
2(Na-Alg)n + n M2+ = (M-Alg2)n + n ( 2Na+) (1)
Solid Electrolyte Solid complex Electrolyte
Where M denotes Mn, Co, Ni, Cu or Zn metals.
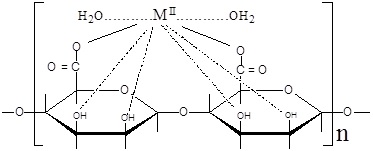
A kind of chelation occurs between the interdiffused divalent metal ions with both the carboxylate and hydroxyl functional groups of the alginate macromolecular chains. This chelation is not just simple, but partially ionic and partially coordinate bonds are formed between the metal ion and the carboxylate and hydroxyl groups, respectively, through sort of bridges. Thus in turn, the chelation will lead to the formation of the corresponding coordination biopolymer complexes in an egg-carton like structure [4,5]. Hence, two configurations of the geometrical structures can be suggested in such chelation [22]. In the first geometry, the functional groups involved in chelation are belonging to the same chains. Hence, the symmetry plane of the gel complex involving the chelated metal ion is parallel with the plane of the alginate macromolecular chains and can be termed by the planar geometry or intra-molecular association. In the second type of geometry, the plane containing the metal ion is perpendicular to the plane of alginate macromolecular chains, i.e. the functional groups are related to different chains. Hence, the geometry is termed by the non-planar geometry and corresponds to the intermolecular association. The priority of the two geometrical structures depends on the nature and valence of the metal ion. The two configurations are shown in (Scheme 1).
Intermolecular Association
Intramolecular Association
Figure 1 showed the FTIR spectra of the metal alginate complexes, whereas the vibrational assignments of the bands are listed in (Table 1). It is clear that bands of the asymmetric stretching vibrations of -OCO- group (υas) are shifted from 1600 cm-1 for alginate to more or less frequencies. On the other hand, the bands of the symmetric stretching vibrations of -OCO- group (υs) were shifted from 1400 cm-1 for alginate to higher frequencies, respectively. This result indicates that the functional groups are participating into the coordination process. Again, the enhancement of the υOH band to lower frequencies is larger and broader than that of alginate for all metal alginate complexes which may indicate that the OH groups take part in chelation. Again, these complexes were found to be amorphous in nature.
Table 1: Infrared frequencies (cm-1) for sodium alginate and cross-linked metal alginate complexes.
|
Compound |
υs OCO |
υas |
υOH |
υM-O |
Ref. |
|
Na-alginate |
1600 |
1400 |
3500 |
850 |
20 |
|
Co(II)- alginate |
1579 |
1415 |
3219 |
816 |
This work |
|
Ni(II)- alginate |
1595 |
1417 |
3450 |
814 |
This work |
|
Cu(II)-alginate |
1604 |
1406 |
3325 |
817 |
This work |
|
Zn(II)-alginate |
1602 |
1411 |
3280 |
816 |
This work |
|
Mn(II)-alginate |
1616 |
1425 |
3480 |
820 |
This work |
Three stages of weight loss (TG) associated with endo- and exothermic peaks (DTA), respectively were clarified from the TG and DTA thermograms thermal decomposition of sodium alginate. The first one of weight loss in the TG curves was attributed to the evolution of coordinated water molecules. The maximum decomposition temperature of the first endothermic and second exothermic peaks (DTA) was found to be nearly similar for all complexes. This means that the decomposition behavior of these complexes proceeds through similar manner [19,20].
Cu (II) Co (II) Mn (II)
Ni (II) Zn (II)
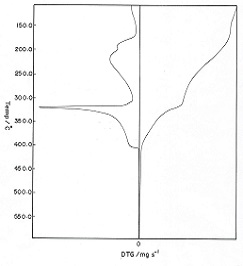
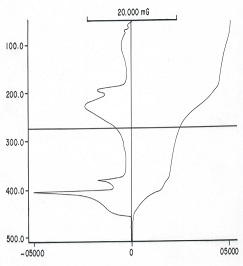
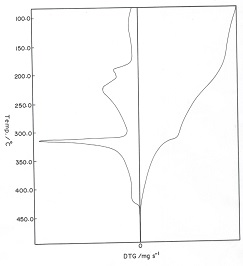
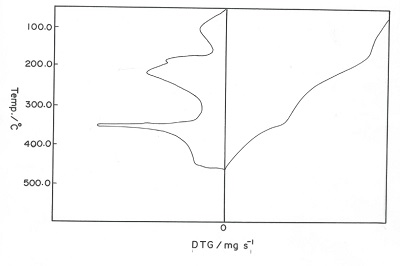
Figure 2: TG and DTG thermograms of the cited cross-linked metal alginate complexes
Figure 2 showed the TG and DTG thermograms of those complexes at heating rate of 20K/min. The TG thermograms showed three decomposition steps for the complexes. The first step corresponds to the dehydration of two coordinated water molecules, while the second and third steps correspond to the decomposition of those dehydrated complexes formed in the first stage. The weight loss and the corresponding temperatures are summarized in Table 2. The weight loss observed was found to be in good agreement with the values that calculated theoretically for the products formed. Whereas, the DTG curves exhibit a series of thermal changes associated with the TG curves. The low temperature corresponds to the elimination of two coordinated molecules in one step seems to be an indication of its weekly coordination in their metal-alginate complexes [23]. The endothermic peaks were explained by the partial degradation and pyrolysis of these complexes to the intermediate compounds, whereas the exothermic peaks were interpreted by the decomposition of the intermediate formed to the corresponding metal oxide [20].
Table 2: The peak temperature (Tp) and the weight loss accompanying the stage of decomposition for cross-linked metal alginate complexes (heating rate = 20K/min)
|
Complex |
Stage |
TGoC |
Weight loss % |
Tp oC |
Formula |
||
|
Ti |
Tf |
Tm |
|||||
|
Mn(II)-alginate |
1st 2nd 3rd |
56 170 340 |
340 557 |
108 205 425 |
9.2 45.2 37.4 |
209 |
C12H14O11Mn.2H2O |
|
Co(II)- alginate |
1st 2nd 3rd |
56 163 305 |
163 305 466 |
114 206 326 |
9.3 40.9 37.3 |
215 |
C12H14O11Co.2H2O |
|
Ni(II)- alginate |
1st 2nd 3rd |
56 172 302 |
172 302 503 |
121 214 317 |
9.6 41.3 34.9 |
218 |
C12H14O11Ni.2H2O |
|
Cu(II)-alginate |
1st 2nd 3rd |
56 165 258 |
165 258 397 |
105 220 314 |
9.7 38.3 40.1 |
223 |
C12H14O11Cu.2H2O |
|
Zn(II)-alginate |
1st 2nd 3rd |
54 159 315 |
159 310 565 |
112 208 356 |
9.9 39.5 36.8 |
211 |
C12H14O11Zn.2H2O |
A suitable reaction mechanism in good consistent with the thermal decomposition may be suggested on the basis of the above aspects and our experimental observations. It involves the dehydration of the water molecules in the first stage,
followed by the formation of metal oxalate as intermediates in the second
Then, the oxalate intermediates formed are decomposed to give rise to the metal oxides as final decomposition product in the third step as follows,
The kinetics of their thermal decomposition depends on the model structure of the formed complex, nature of metal ion, strength of chelation and orientation of the macromolecular chains of alginate toward the chelated metal ion since these metal-alginate complexes have a rigid network of linear block structures. Sestak and Berggen [24] and Satava [25] have discussed how to evaluation of the reaction mechanism by non-isothermal methods. This method is based on the assumption that non-isothermal reactions proceed in infinitesimal time intervals and, hence, the rates can be expressed by the Arrhenius type equation
where Z is the frequency factor, t is the time, α is the decomposition fraction, and F(α) depends on the mechanism of the process.
A theoretical method for the reduced time was suggested by Sharp and co-workers [26] in order to distinguish between the different methods where the time scales in the kinetic equation is
where g(α) is the integrated form of F(α) which altered so that
Here t0.5 is the time for 50% decomposition and A is a constant depending on the form of g(α)
The determined t0.5 which corresponds to α = 0.5 (using the experimental data) was used to convert the data to curves of the form α - (t / t0.5) plots. Linear regression analysis was applied to analyze the non-isothermal data according to various kinetic model functions [24]. Table 3 summarized the best fitting models of the hydration processes for the investigated samples.
Samples of 10 mg were used at the three heating rates 5,10 and 20 K/min in order to obtain reliable kinetic parameters. However, different methods may be used to calculate the kinetic parameters. The following equation was applied in the present study
where Φ is the heating rate, E is the activation energy, T is the absolute temperature, Tp is the peak temperature of decomposition and R is the gas constant. Equation (8) was based on a proposed reaction mechanism given by Satava together with Coot’s-Redfern equation [27]. The g(α) assumes different forms to describe the rate process depending on the model applied. Plots of log g(α)/T2 against 1/T should be linear as was observed experimentally from which slopes and intercepts, the activation energy and frequency factor can be determined. These values were calculated by using the method of least- squares and are summarized in Table 3.
Again, the entropy of activation can be evaluated from the following relationship [27]
where kB is the Boltzmann’s constant and h is the Planck’s constant. The values of entropies of activation are listed in Table 3. The observed negative values of entropies of activation with respect to all cited complexes with respect to the initial dehydration step may indicate that the activated complexes formed during the dehydration processes are more ordered than that of the reactants, in good agreement with that reported earlier for some other divalent metal alginate complexes [20].
The magnitude of the activation energies and the maximum temperatures of decomposition shown in (Table 2 & 3) may be indicative to the stability of these complexes. The stability was found to increase in the order Zn < Mn ≤ Co < Ni < Cu–alginates, in good agreement with their magnitudes of M-O bond energies [28] and with the same order of magnitude reported elsewhere [16,18,29-31]. The high stability of cross-linked copper-alginate complex may be attributed to its distorted octahedral structure and high degree of orientation [17].
Table 3: Kinetic parameters for non-isothermal decomposition of cross-linked metal alginate complexes.
|
Complex |
Heating rate K/min |
Kinetic model |
E≠,kJmol-1 |
∆S≠,JKmol-1 |
Log Z, |
|||||||||
|
Stages |
||||||||||||||
|
1st |
2nd |
3rd |
1st |
2nd |
3rd |
1st |
2nd |
3rd |
1st |
2nd |
3rd |
|||
|
n(II)-alginate |
5 10 20 |
F1 F1 F1 |
A3 A3 A3 |
R3 F1 R3 |
95.4 102.5 116.7 |
165.4 178.2 200.1 |
230.4 245.5 299.1 |
-45.4 -39.9 -38.8 |
34.7 43.8 17.6 |
64.3 57.9 72.5 |
10.5 10.8 10.9 |
13.0 13.7 13.9 |
15.5 16.2 16.8 |
|
|
o(II)- alginate |
5 10 20 |
F1 F1 F1 |
A3 A3 A3 |
A3 A3 A3 |
100.1 80.4 120.1 |
200.8 212.1 180.7 |
305.8 290.7 240.5 |
-93.6 -86.5 -81.4 |
19.9 73.6 14.7 |
95.56 89.6 37.2 |
8.0 8.4 8.7 |
14.4 14.9 13.8 |
18.1 17.8 15.0 |
|
|
Ni(II)- alginate |
5 10 20 |
A2 A2 A2 |
A3 A3 A3 |
A3 --- A3 |
99.8 116.4 105.6 |
207.6 215.1 224.3 |
312.1 ---- 316.4 |
-66.6 -45.9 -72.1 |
25.1 49.2 23.1 |
98.0 ---- 81.0 |
9.4 10.5 9.1 |
14.3 13.5 14.2 |
18.2 ---- 17.3 |
|
|
Cu(II)-alginate |
5 10 20 |
A3 A3 A3 |
R3 R3 R3 |
--- --- --- |
168.5 199.7 180.5 |
220.2 232.5 230.6 |
--- --- --- |
-37.4 -22.8 -12.9 |
25.4 47.9 51.0 |
--- --- --- |
11.04 11.8 12.3 |
14.3 15.2 15.7 |
--- --- --- |
|
|
Zn(II)-alginate |
5 10 20 |
A3 A3 R3 |
R3 R3 F1 |
R3 R3 R3 |
80.6 76.9 100.4 |
150.1 160.3 140.4 |
310.1 320.4 290.1 |
-83.0 -110. -34.9 |
20.7 34.1 18.6 |
94.4 105.3 56.7 |
8.5 7.1 11.1 |
14.8 14.8 12.0 |
18.1 18.6 16.1 |
|
The influence of heating rates on the thermal decomposition (5,10 and 20oC ) was examined. The peak positions were found to be shifted with the increase in temperature. The observed linearity between log Z values and E values indicates the demonstration of the kinetic compensation effect.
Conflicts of interest
There are no conflicts to declare.
REFERENCES
- Chanda SK, Hirst EL, Percival EGV, Koss AG (1952) J Chem Soc 1833.
- Wistler RL, Kirby KW (1955) Z Physiol Chem 314: 46.
- Fisher FG, Dorfel H (1955) Z Physiol Chem 302: 186.
- Rees DA (1972) Shapely polysaccharides. The eighth colworth medal lecture. Biochem J 126(2): 257-273.
- Morris ER, Rees DA, Thomas D (1978) Carbohyd Res 66: 143.
- Haugh A, Smidsrod O (1965) The Effect of Divalent Metals on the Properties of Alginate Solutions. II. Comparison of Different Metal Ions. Acta Chem Scand 19: 341-351.
- Haugh A, Larsen B, Smidsrod O (1974) Uronic acid sequence in alginate from different sources. Carbohyd Res 32(2): 217-225.
- Smidsrod O, Haugh A (1965) The Effect of Divalent Metals on the Properties of Alginate Solutions. I. Calcium Ions. Acta Chem Scand 19: 329-340.
- Thiele H (1948) Z Natureforeschang 36: 778.
- Thiele H (1954) Koll Z 130: 80.
- Hassan R M, Wahdan MH, Hassan A (1988) Eur Poly J 24: 281.
- Hassan RM, El-Shatoury SA, Mousa MA, Hassan A (1988) Eur Poly J 24: 1173.
- Hassan RM, Summan A, Hassan M K, El-Shatoury SA (1989) Eur Poly J 25: 1209.
- Hassan RM, Makhlouf MTh, El-Shatoury SA (1992) Coll Poly Sci 270: 1237.
- Hassan RM, El-Shatoury SA, Makhlouf MTh (1992) High Perf Poly 4: 49.
- Hassan RM, Makhlouf MTh, Summan AM, Awad A (1989) Eur Poly J 25: 993.
- Hassan RM, Awad A, Hassan A (1991) J Poly Sci 29: 1645.
- Hassan RM (1991 & 1993) J Mater Sci 26: 5806 & 28: 384.
- El-Gahami MA, Khairou KS, Hassan RM (2003) Bull Polish Acad Sci 61: 105.
- Said AA, Hassan RM(1993) Poly Degrad Stab 39: 393; Said AA, Abd El-Wahab M MM, Hassan RM (1994)Thermochim Acta 233: 13.
- JKAU Sci., Saudi Arabia, 22: 193.
- Hassan RM (1993) Poly Inter 31: 81.
- Eugena ACC, Carvalho (1971) J Therm Analy 2: 269.
- Sestak JL, Berggen G (1971) Thermochim Acta 3: 42.
- Satava V (1966) Thermochim Acta 2: 379.
- Sharp JP, Brindley GW, Achar BNN (1966) Am Ceram Soc 49: 379.
- Coots AW, Redfern JP (1964) Nature 20: 68.
- Sanderson RT (1976) Chemical Bonds and Bond Energy [2nd Ed.], Academic Press, New York.
- Schewiger R (1964) Koll Z 196: 47.
- Smidsrod O (1965) Acta Chem Scand 19: 329.
- Hassan RM, Summan AM, Hassan MK, El-Shatoury SA (1989) Eur Poly J 25: 1209.
Copyright: Hassan RM, et al. ©2019. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Citation: Hassan RM (2019). Degradation Kinetics of Some Coordination Biopolymers of Transition Metal Complexes of Alginates: Influence of Geometrical Structure and Strength of Chelation on the Thermal Stability. Material Science 1(1): 3.
 Abstract
Abstract  PDF
PDF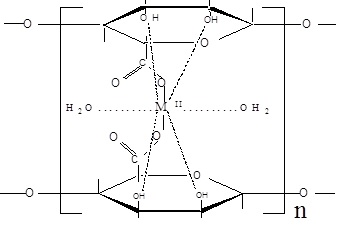
.jpg)
.jpg)