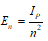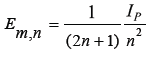Current Issue
Hydrogen Molecule: Estimation of the Ground and Excited Electronic States
Asif Zaidi*
Adjunct Faculty, Physics and Astronomy at University of Waterloo, 200 University Avenue West, Waterloo, ON, Canada
*Corresponding author: Dr. Asif Zaidi, Adjunct Faculty, Physics and Astronomy at University of Waterloo, 200 University Avenue West, Waterloo, ON, Canada, Phone: +1 519 888 4567, E-mail: [email protected]
Received Date: March 14, 2025
Publication Date: April 22, 2025
Citation: Zaidi A. (2024). Hydrogen Molecule: Estimation of the Ground and Excited Electronic States. Material Science. 7(1):37.
Copyright: Zaidi A. © (2024).
ABSTRACT
Considering electron Compton wavelength associated with the mass of an electron as a basic unit of length for atomic and molecular systems one can estimate electronic energy levels of atomic and molecular systems by simple consideration of the atomic or molecular bound state as a standing wave. This investigation is about the calculation of both ground and excited electronic energy levels of hydrogen molecules accurately without complex quantum mechanical calculations based on the particle model. Predicted molecular electronic energy levels are obtained by a simple multiple of atomic ground state number of Compton waves. As hydrogen is now part of environmentally safe fuel research, simple and accurate investigation of its ground and excited states is useful. This paper establishes molecular energy level calculations using well-known corresponding atomic parameters atomic ionization potential and Bohr’s principal quantum number.
INTRODUCTION
Atomic and molecular energy calculations are useful for many physical and chemical studies of atoms and molecules. Hydrogen molecule being the simplest molecule is interesting to study for its physics and its new importance due to its clean energy source. This article is about extending hydrogen molecule’s energy calculation for excited states. Electronic ground state calculations, of molecular hydrogen, involving the solution of the Schrodinger equation using quantum mechanics are complex calculations and the results are approximate. James and Coolidge have done a thirteen-term approximation [1,2].
Electron Compton wavelength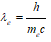
Symbols have usual meanings such as “c” for speed of light in free space, “h” as Planks constant “me” electron mass, and λe wavelength associated with the electron. The numerical value of the reduced electron Compton wavelength is 3.861 x 10-13 m. In the ground state of the hydrogen atom, the ratio.The ground state of the hydrogen atom contains exactly 137 Compton waves and one de Broglie wave. In this paper, all molecular energy states of hydrogen, ground, and excited states have been calculated using some multiple of the number of Compton waves in the atomic ground state of the hydrogen atom.
The Value of the first, excited state calculated and experimentally observed was published by Ernest Davidson [3]. Calculations based on the standing wave model are closer to the experimental value. More recently potential curves for the hydrogen molecule published by Anatoly S et al allow estimation of the ground and excited states of hydrogen molecule [4].
MOLECULAR HYDROGEN: ELECTRONIC STATES
The electronic ground state of the hydrogen molecule using a standing wave model based on electron Compton wavelength as a basic unit of length for atomic and molecular systems has been discussed in detail by Zaidi A. A. [5]. In the molecular ground state energy estimation for hydrogenic systems considering standing waves one needs to know the number of waves in an electronic state. This can be done by calculating the difference between the number of waves in the corresponding atomic ground and the first excited state. Concludes molecular ground state energy estimation as.
Nm is the required number of Compton waves in a molecular state. While and are numbers of waves in the first excited and the ground atomic state. In terms of Bohr's principal quantum number N=137 n2. Using this in (1),
Molecular excited states are given by [6],
n = 1,2,3...., is Bohr’s principal quantum number for atomic hydrogen. Here nm represents the molecular state quantum number, which in terms of Bohr’s Principal quantum number can be represented as (2n+1).
Where “n” is the Bohr’s principal quantum number. Here ionization potential of the ground atomic orbit can be expressed as
V0 is the ionization potential of the atomic ground state -13.609 eV. Similarly, the atomic ionization energy of excited atomic states is given by, V0 /n2.
Where: n = 1,2,3....,is Bohr’s principal quantum number.
Equation (6) contains molecular ground and excited state values, and equation (7) contained in equation (6) represents the ionization potential of the hydrogen atom in the ground states. Equation (8) represents molecular ground and excited states in terms of atomic parameters like ionization potential and respective Bohr’s Principal quantum numbers.
To further simplify equation (8), atomic ground state ionization potential is 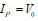
n = 1,2,3...., represents atomic states Bohr’s principal quantum number and nm = 3,5,7 indicates molecular energy states. Replacing nm = (2n+1),
n = 1,2,3.........is Bohr’s principal quantum number for respective atomic states.
Equation (10) represents molecular electronic energy levels ground state and other excited states.
Em,n represents the molecular ground and excited states determined by higher “n.”
Values like Em,2, Em,3.......
Ground State of hydrogen molecule:
Where n = 1 represents the molecular ground state of the hydrogen molecule and 2,3,4, represents molecular excited states. Ip is the ionization potential for the atomic ground state – 13.609 eV.
n =1, nm = (2n+1) = 3 and Ip = -13.609 eV. These yields for the first molecular ground state,
Em,1 = - 4.536 eV.
First excited state:
n= 2, nm = 5 and Ip = -13.609 eV
Em,2 = - 0.680 eV
Other higher molecular energy levels can be calculated using equation (10), by basically using atomic parameters and molecular state values nm- = (2n+1). Calculated values and accepted values are in the table 1.
Table 1. Theoretically calculated ground state and first three excited state energy levels for Hydrogen molecule and accepted experimental values
|
Molecule H2 |
Molecular Energy Em (eV) (Calculated) |
Molecular Energy Em (eV) (Accepted) |
% Error |
|
Ground State n = 1 |
- 4.536 |
- 4.556 |
0.44 |
|
Ist excited state n = 2 |
- 0.6805 |
- 0.6935 |
1.875 |
|
2nd excited state n =3 |
- 0.216 |
-0.2721 |
20.61 |
|
3rd excited state n = 4 |
-0.0945 |
-0.0886 |
6.66 |
CONCLUSIONS
Molecular ground and excited energy values for the hydrogen molecule can be calculated accurately only by knowing the hydrogen atom’s two parameters atomic ionization potential and Bohr’s principal quantum number for the hydrogen atom. This indicates that the standing wave model based on electron Compton wavelength treating bound electron as a vibrating string provides remarkable simplicity and significant accuracy without using approximations. This method gives simple relations for atomic as well as molecular hydrogen as
where n = 1,2,3,4… And.PNG)
H2: molecular electronic states.
m = (2n+1).
.PNG)
ACKNOWLEDGMENTS
I want to thank Professor Khursheed Siddiqi and Dr. M. Nadeem Iqbal for discussing this subject in detail and the useful suggestions.
CONFLICT OF INTEREST
The author declares that there is no conflict of interest.
REFERENCES
- Compton AH. (1923). The Spectrum of Scattered X-Rays. Phys Rev. 22:409.
- James HM, Coolidge AS. (1933). The Ground State of the Hydrogen Molecule. A S J Chem Phys. 1:825.
- Davidson ER. (1961). First excited state of hydrogen molecule. J Chem Phys. 35:1189-1202.
- Svidzinsky AA, Scully MO, Herschbach DR. (2005). Simple and surprisingly accurate approach to the chemical bond obtained from dimensional scaling. Phys Rev Lett. 95(8):080401.
- Zaidi AA. (2023). Atomic and Molecular Ground State Energy Estimation of Hydrogen and Hydrogenic Molecules. Material Science. 5(1):18. March 30, ISSN: 2690-2532. DOI: https://doi.org/10.35702/msci.10018.
 Abstract
Abstract  PDF
PDF.PNG)
.PNG)
.PNG)
.PNG)


.PNG)
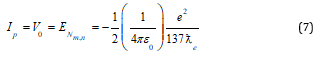
.PNG)
.PNG)