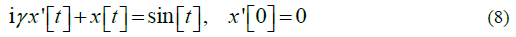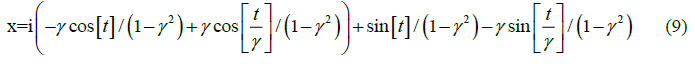Past Issues
Foundations of Magnetic Field Definition
Stanislav Ordin*
The Russian Academy of Sciences, Russia
*Corresponding Author: Stanislav Ordin, The Russian Academy of Sciences, Russia; Email: [email protected]
Received Date: May 10, 2024
Publication Date: June 10, 2024
Citation: Ordin S. (2024). Foundations of Magnetic Field Definition. Material Science. 6(1):27.
Copyright: Ordin S. © (2024).
ABSTRACT
The fundamental physical contradictions of the canonized Definition of the Magnetic Field and mathematical errors in the foundations of its description were given in previous works. Here they are generalized and the incompleteness of the previously used orthogonal reference point of the Magnetic Field Description is shown. But, before giving its corrected definition, it was necessary to consider the model of the new Oscillator, taking into account fragments of previously introduced models relating to the general dynamics of the Magnetic Field. In this work, it was found that, in contrast to the conditional complexity of solutions of a real Harmonic Oscillator, the orthogonality of the Magnetic Field leads, due to reactive damping, to the emergence of true complexity of its equation of motion itself, and to complex oscillations (harmonics). These obtained solutions reflect the orthogonality of the Ampere-Lorentz Force to the electric field.
Keywords: Orthogonal Frame, Oscillator, Real Solution, Complex Solution, Orthogonal Ampere Force
INTRODUCTION
Any field, by definition, is Force, which is a continuous parameter of space. For the Magnetic Field, this parameter is the Ampere Force, but it was actually neglected. Without fully understanding the elementary Lorentz Force, the mystical “Theory” of Magnetism was built.
The theory of interaction of Descartes’ “gimlets”, which was used by Maxwell to build generalelectrodynamics.This,strictlyspeaking,ledtotheuncertaintyoftheveryconceptoftheMagneticField. So in practice, when designing magnets, the “Theory” of magnetism actually did not workandwasusedbyKirchhoff’srulesbasedonempiricalparameters.Theanalysisoftheelementaryelectricoscillatormadeitpossibletounambiguouslyconnecttheimaginarytermsofthecompletesolutionofthedifferentialequationofthecomplexelementaryoscillatorwiththeimaginaryparameterinitiallyintroducedintoitsequation,whichstrictlycorrespondstotheorthogonalelectricfield-magnetic.Andthismadeitpossibletorestorethecorrectpictureofthemagneticfield.
Invariant BASIS and Magnetism
In modern science, since the description of fragments on the basis of local, purely empirical laws is often used, and not a single axiomatic approach on the bASE of a strictly established orthogonal frame, many contradictions have accumulated. Likewise, the magnetic field, widely used in modern science and technology, which is one of the benchmarks, because of his imaginary “exceptionalism” [1], there is still not even an unambiguous definition of it. That is why specialists who use the magnetic field in practice invest in its understanding what is more familiar to them - either H or B. This leads to confusion in the development of magnetic materials. And for practical calculations of devices such as electromagnets on the Tokamak, and on the LHC, and in the MRI, and on magnetic levitation trains, they use technical rules of thumb from the “Theoretical Fundamentals of Electrical Engineering,” which are borrowed from the design of electromagnets for loading scrap metal. So it is not at all by chance that in the modern theory of magnetism there are many contradictions and inconsistencies, even such large ones as the discrepancy between the electromagnetic and optical descriptions. And in work [2] the most fundamental reasons for the need for a strict determination of the magnetic field were shown. But there are enough contradictions in the classical description of magnetism to try to forget about entire volumes of “mental” constructions in which they tried to eliminate the contradictions in the basis of the modern classical theory of magnetism by the method of adjustments. The basis must be chosen initially consistent so as not to hide behind additional quantum conditions in the very definition of the magnetic field. Whereas theorists, claiming that without quantization it is generally impossible to explain Magnetism, act, making a phenomenological mistake, exactly the opposite. And the age-old misconceptions in the basics of quantization and the theory of relativity, as shown earlier, arose due to the fact that ideas about the magnetic field are inherent in their original form, like the “gimlets of democritus” passing through the spiral channels of the Earth from the “North Pole” to "South Pole". And this entailed that “gimlets” were recorded in Science, even in Mathematics for hundreds of years.
But, after the bridge was thrown from quantization to relativity, it became obvious that one of the reasons for the fundamental difficulties is the finiteness of the speed of light, which they have in common. So both quantization and SRT require clarification of the basis, which includes the very definition of the magnetic field. After all, it was this that initially demonstrated the finiteness of the speed of light. And if we start in the definition of the magnetic field from Ampere’s law, which actually describes the magnetic force, proportional to the relative speed of electrons, then it follows that this is simply the force of interaction between moving charges. According to Ampere, it is positive if the charges move parallel and in one direction and negative if they move antiparallel - counter. If we recall Galileo’s Principle of Relativity, then Einstein introduced a correction to SRT for charges moving relative to each other only for mass. And if for charges stationary relative to each other there is only the Coulomb force, then between moving charges, in addition to the Coulomb force, an additional force arises, perpendicular to the relative speed, proportional to the relative speed of movement of the charges. And the main question that divided scientists into two believing sects is the question of what to consider the movement of both light and a pair of charges in relation to a stationary observer or relative to the environment. But this “paradox” is also removed if initially, in strict accordance with the Principle of Causality, we take into account the finiteness of the rate of change of the Coulomb field when a charged particle is displaced. At the same time, the imaginary paradox about the absence of interaction between orthogonal coordinates is also eliminated - simply the energy for each of them is calculated through the product of collinear forces and coordinates.
Elementary Complex Oscillator
In previous works, the elementary oscillator was analyzed on the basis of the mechanical oscillator. For the differential equation of this oscillator, a complete real Solution was obtained, which is of a general character for any modifications of the oscillator [3,4]. And it was shown that the complex parameters artificially introduced into Newton’s partial solution for the real oscillator are purely conditional. Imaginaries can be used only under strictly specified conditions. This was simply a technical technique for approximately finding the independent real parameters of a particular solution on the complex plane. This purely mathematical confusion in complex particular solutions can, as will be shown in this paragraph, be identified and eliminated, taking into account the physical properties of the magnetic field.
To do this, consider two different modifications of the elementary electric oscillator. In one, the so-called Plasma - Basic Optical Model, which describes the reaction of free electrons to radiation (electromagnetic), the electric oscillator is a modified elementary mechanical oscillator, only the rigidity force for charged particles is determined not by a mechanical spring, but by the electric field created by the charges themselves displaced onto the plates (Figure 1a). In another basic electrical model of the oscillator built using purely empirically established technical parameters: capacitance of the capacitor and inductance of the coil, oscillations are described not in the position of charges, but in oscillations of currents in the circuit (Figure 1b).
Figure 1: A model with gravitational (m) inertial force and electrostatic (E) rigidity force determined by the electron concentration n (a) and a model with a magnetic inertial force determined by inductance L and capacitor C (b).
For comparison, the basic formulas describing these two models are given in Table 1.
Table 1: The balance of forces or energies, previously described by one Newton harmonic, the change in the position of charges (in the Plasma model) and the change in currents (in the Skin layer model).
Table 1 is summary, each column represents an elementary Model, described in many primers. The value of the table is that it shows the correspondence and difference in the descriptions of oscillations of displacements and velocities.
In work [5], the limits of applicability of these models were analyzed, when going beyond the limits of applicability of which a borderline “Catastrophe” appears in the description, similar to that eliminated by Planck [6]. Without realizing the very existence of this “catastrophe” in optics, they always tried to eliminate the “errors” associated with it using the Landau smallness parameter (which, in principle, is not true for giant effects [7]). And in electrodynamics, the same approach of adjustments was veiled by the distance of electromagnetic waves from the emitter, which even tried to justify the coincidence of the phases of the electric and magnetic fields in them. The distance from the emitter of the electromagnetic wave actually hides the fact that both in the emitter itself and in the waves emitted by it there is no instantaneous disappearance of energy, which is obtained without any adjustments for the current and voltage shifted in phase by a quarter of the period, the sum of their energies is - squared amplitudes constant. The product of instantaneous (strength) current and instantaneous (“strength”) voltage is not instantaneous total electrical power
-it is only a technical method for determining electrical power by the product of effective (equivalent to constant) amplitudes of current and voltage.
Formally, the force balance equation of the plasma model (in the table on the left) can be transformed (by taking the derivative) into the equation of the skin layer model (in the table on the right). But this is not the basis for the identity of these equations. This is only a manifestation of the applicability of the principle of logarithmic relativity to the very model of the elementary oscillator for different degrees of derivatives. This “logarithmic” approach was actually used earlier when describing processes using quasiparticles. But under certain boundary conditions (frequencies), mixed vibrations can also play a significant role, for which strict separation of derivatives does not work. Planck described them with the quantum of energy of resonant electromagnetic waves, but purely statistically. And in order to strictly mathematically describe mixed oscillations, it is necessary to take into account all the terms of the equation used in both models, but separately. From a comparison of the equations it is clear that in the plasma model (on the left) the inertial force proportional to the current is neglected, and the force proportional to the mass of charges, which is neglected in the skin layer ,model, can act as a kind of rigidity.
These neglects are acceptable in different oscillation frequency ranges. Since static gravitational forces are 42 orders of magnitude weaker than electrostatic forces, their comparison by order of magnitude in the equation on the left is possible only at very high frequencies, when the inertial force due to large accelerations is large. Of course, if we assume that the electric force does not depend on frequency - on the acceleration of the charge. The latter, in fact, is indicated by the fact that the plasma model well describes the high-frequency edge of plasma reflection by free carriers in metals and semiconductors. But to what extent the inertia of the charge itself is negligible is still an open question [8]. And an additional circumstance that helps equalize the electrical force and the force of gravitational inertia is the high concentration (total mass) of electrons in metals with a small charge that inhibits this entire mass of electrons in a volume proportional to the displacement of electrons in a thin surface layer. It should also be borne in mind that when photons are specularly reflected from a plane for free carriers, there is no real (model, perpendicular to the electric field) boundary on the plane. The role of the boundary is played by locally compressed electrons themselves - plasma waves. And the artificial creation of boundaries perpendicular to the electric field leads to the formation of a spatial Oscillator below the cutoff frequency and to diffraction effects above the cutoff frequency.
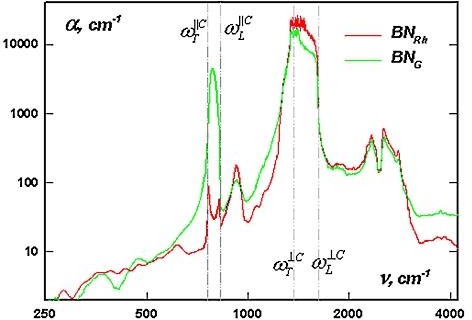
Traditionally, the introduction of a term proportional to velocity into the Oscillator equation means friction, the contribution of which, as is known, determines the damping of oscillations. Valid solutions for the elementary oscillator. Modifications of the elementary oscillator equation to take into account additional forces were carried out earlier, but due to a parametric change in the rigidity force [9]. Those influences are orthogonal to the forces traditionally used in balance was implicitly implied. But the orthogonal force, initially believed, does not produce work (although in reality the force and displacement for each coordinate separately should be collinear). The zero energy coupling of forces clearly violated Logic, but qualitatively the model of a parametric oscillator made it possible to describe a number of effects. Although, formally, using Mathieu functions, it did not provide an answer to the physical question, and the observed absorption at the vibration frequency along the wave vector of light (Figure 2) indicated the exchange of energy between normal vibrations in anisotropic crystals [10].
In a rhombohedral boron nitride single crystal, when light propagates along the symmetry axis C, in the transmission spectrum, in addition to the normal absorption band in the frequency range of optical phonons polarized perpendicular to the C axis, w^C ¸w^C a non-transmission band anomalous in frequency wIIC ¸wIIC and shape was discovered.
Figure 2: IR absorption spectra of rhombohedral and hexagonal (with disordered crystallites) boron nitride measured at normal incidence of unpolarized radiation on plates perpendicular to the C axis.
In the absorption spectrum of a weakly ordered textured sample of hexagonal boron nitride shown in Figure 2, in which the C axis of its crystallites is deviated from the wave vector of light, the classical crystal-optical contribution to the absorption of vibrations along the C axis appears in the form of a normal absorption band between the transverse and longitudinal vibrations corresponding to interlayer vibrations phonons. Whereas for a highly ordered single crystal of rhombohedral boron nitride, instead of this usual absorption band, only scattering peaks are observed at phonon frequencies, the polarization of which is orthogonal to the polarization of IR radiation.
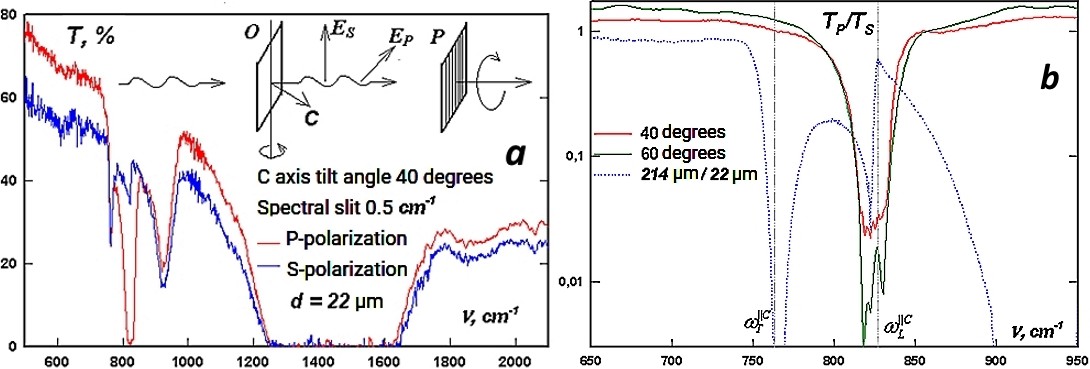
Figure 3: Dependence of the ratio of the P- and S-components of unpolarized radiation transmitted through an oriented sample of rhombohedral boron nitride on the thickness of the sample and on the angle of rotation of the C axis relative to the wave vector of light.
The inset to Figure 3 shows the setup of a polarization experiment to analyze the P- and S- components when the C axis of rhombohedral boron nitride deviates from the direction of light propagation.
Precision polarization measurements of highly ordered crystals of rhombohedral boron nitride presented in Figure 3 made it possible to associate the anomalous stopband in it with scattering by orthogonal vibrations. And although this did not give a direct answer to the question of the reverse transfer of energy between them, it nevertheless indicated the incompleteness of the description of the causality principle by the Kramers-Kronig relation without taking into account the contribution of orthogonal oscillations, at least scattering by them.
But in an electromagnetic wave, not just scattering occurs, but energy transfer between orthogonal oscillations. And from a comparison of the models of two electric oscillators and their equations (Table 1) it is clear that in both of them, separately, this is not taken into account. The plasma model does not take into account the inertia of current, and the electrical model does not take into account the inertia of mass, which, as noted above, is permissible only within the limits determined by the limits of applicability of the models.
And, at the same time, since it is ignored that the unaccounted orthogonal terms are directly related to the exchange of energy between orthogonal oscillations, we will not complicate the existing oscillator models with additional terms. For now, we will limit ourselves to considering a fundamentally new electric oscillator with an additional, previously unaccounted for member. And the introduced new reactive force orthogonal to the electric field, proportional to the speed (current), will be taken into account using imaginity. So let's consider another modification of the elementary oscillator - the complex electric Ideal oscillator based on the balance of only two orthogonal forces.
In this simplest model case, we obtain the balance equation of the real electrical force and the imaginary magnetic force orthogonal to it. In this case, we have the oscillator equation for the real and imaginary (orthogonal to the electric force) charge displacement x, standardly excited by a single initial condition:
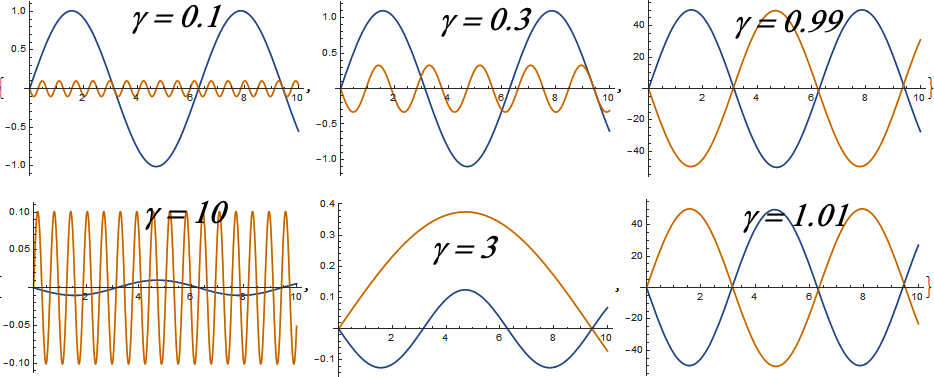
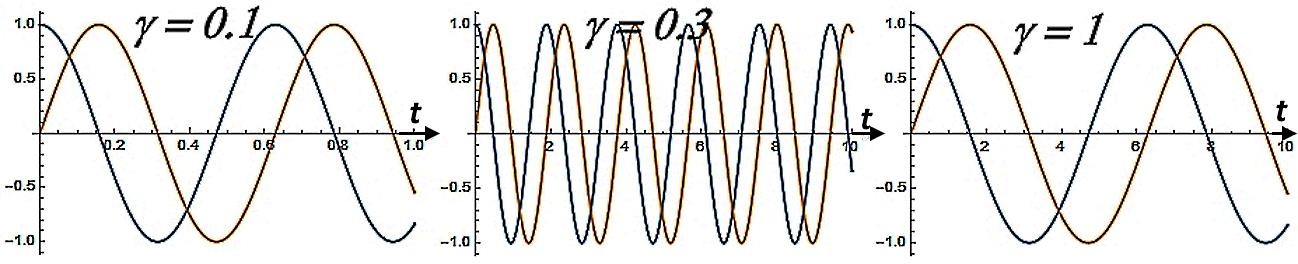
His solution gives harmonic, but phase-shifted by a quarter of the period, oscillations of two orthogonal forces at one single resonant frequency W , determined by the reactive “friction” g the reactive coupling of the forces (Figure 4)
Figure 4: Associated resonant oscillations of two Orthogonal Forces, the single frequency of oscillations of which is determined by the reactive connection of these Forces.
The considered simplest equation with reactive “friction” actually gives oscillations of two orthogonal forces even at zero gravitational mass. And it corresponds to oscillations of two orthogonal forces exchanging energy, which is what happens in an electromagnetic wave, without any instantaneous loss of energy.
For simplicity, the solution of the equation with the reactive coupling coefficient at a unit stiffness coefficient was obtained. If we return to the designations of the coefficients of the equation from table 1, it will become clear that the frequency of natural oscillations of the Complex Oscillator is equal to the ratio of the stiffness coefficient x to the coefficient of reactive damping of the stiffness b (without the square root, as for the real oscillator)
Now let’s consider the action on the Ideal Complex Oscillator of a single driving Force. But first, let us recall that its action on the actual oscillator: manifests itself in the fact that a driving force of any frequency excites in the real oscillator both oscillations at the frequency of the driving force (Newton’s harmonic) and oscillations at its own resonant frequency
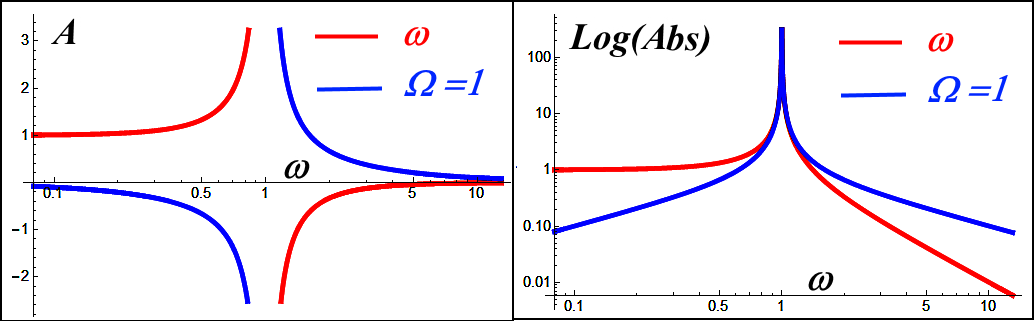
And these two harmonics have different dependences, shown in Figure 5, on the frequency of the driving force, where the resonant frequency is taken as a unit of frequency measurement.
Figure 5: Frequency dependences of the amplitudes (left) and amplitude modulus (right) of Newton's harmonics (red curves) and oscillations at the resonant frequency (blue curves).
For an ideal complex oscillator (with purely reactive friction, in accordance with formula (3), the action of a single driving force is described by the expression:
In this case, for the ideal complex oscillator we obtain the same as for the ideal real oscillator solution from two harmonics, but for both the real and imaginary parts of the oscillations. In this case, both imaginary harmonics are shifted relative to the corresponding real harmonic by a quarter of the period:
Taking, for clarity, the resonant frequency and amplitude of the driving force as unity, we obtain the dependences on the frequency of the driving force of the amplitudes of real and imaginary oscillations of the Ideal Complex Oscillator, both at the frequency of the driving force (Figure 6, left) and at the resonant frequency (Figure 6, on right):
Figure 6: Frequency dependences of the harmonic amplitudes of the Complex Ideal Oscillator.
In a simplified notation with a single resonant frequency, instead of expression (6) we have:
and we obtain the relative change in the harmonics of the Complex Ideal Oscillator), similar to formula (2):
For real harmonics this change, similar to Figure 4, is shown in Figure 7.
|
|
|
|
Figure 7: Relative change in the Real harmonics of the Complex Oscillator.
Changes in the imaginary (shifted by a quarter of the period relative to the Real) harmonics of the complex oscillator are also obtained similar to those shown in Figure 7.
Thus, we obtain for the ideal complex oscillator and under the influence of the driving force of the pair, exchanging oscillation energy. Moreover, each of these two pairs consists of a real oscillation along the oscillator axis and an “Imaginary” oscillation orthogonal to the Real oscillation, phase-shifted by a quarter of the period. And the “imaginary” arose earlier from orthogonality, and not due to the fact that the Magnetic Force is not the interaction of descartes’ “gimlets”, simply mathematized by Maxwell.
CONCLUSIONS
Purely technically, the analysis shows that the true “imaginary” (in the sense of orthogonal) solutions strictly correspond to the imaginary term initially introduced into the differential equation, corresponding to the magnetic field, orthogonal to the electric field, but exchanging energy with it.
Thus, a qualitatively described mechanism of the formation of the magnetic field can also be described on the basis of the elementary oscillator model, cleared of the husk of “Imaginary” solutions for the real oscillator, but supplemented with an imaginary term strictly corresponding to the orthogonality of the Forces, the balance of which leads to a set of interconnected oscillations.
Elimination of this confusion with imagines allowed us to make a correct macroscopic redefinition of the magnetic field.
REFERENCES
- Ordin S. (2024). Exceptionality Exclusion: Bridging Quantization and Relativity. Global J Sci Front Res: A, Physics Space Sci. 24:5-65.
- Ordin S. (2023). Reasons for Redefining the Magnetic Field. J Electro Analy Appl (JEMAA). 15.
- Ordin S. (2021). Non-Elementary Elementary Harmonic Oscillator. Am J Mat Appl Sci(AJMAS). 3:3-8.
- Ordin S. (2024). Comprehensive Analysis of the Elementary Oscillator. J Electromag Analy Appl (JEMAA). 15(4). NRS.000869.
- Ordin S. (2024). Comprehensive Analysis of the ELEMENTARY Oscillator. SSRG-Int J Math Trends Tech.
- Ordin SV. (2020). Impedance of Skin-Plasma Effect. Int J Res Stud Electrical Electronics Engineering (IJRSEEE):25-39.
- Stanislav Ordin. (2020). Planckian Expansion of the Heaviside Impedance. Int J Res Stud Electrical Electronics Engineering (IJRSEEE). 6(3):1-15.
- Ordin SV. (2011). Optical Lattices: Structures, Atoms and Solitons, “Giant spatial dispersion in the region of plasmon-phonon interaction in one-dimensional- incommensurate crystal the higher silicide of manganese (HSM)”, Editors: Benjamin J. Fuentes, Nova Sc. Publ. Inc:101-130. Series: Lasers and Electro-Optics Research and Technology, Physics Research and Technology, Binding: Hardcover, Pages: 241.
- Ordin S.V. (2019). Newton's Coulomb Laws. Global J Sci Front Res Phy Space Sci (GJSFR-A). 19:145-155.
- Ordin SV. Parametrically excited Anharmonic Oscillator. Global J Sci Front Res Phy Space Sci. 19:133-144.
- Ordin SV, Sokolov IA, Zjuzin AJ. (2016). Parametrical Interaction of Normal Oscillations in anisotropic crystals. The Physico-Technical institute of A.F. Ioffe of the Russian Academy of Sciences, St.-Petersburg, Russia, Proceedings of X interstate seminar: Thermoelectrics and their application:144-149.
 Abstract
Abstract  PDF
PDF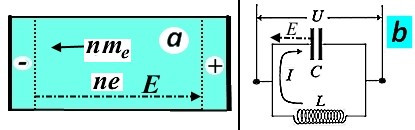
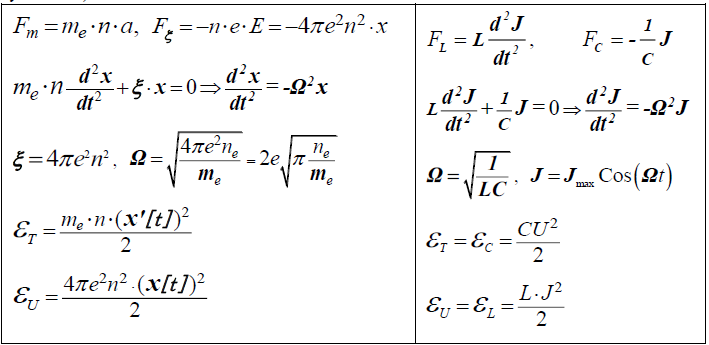
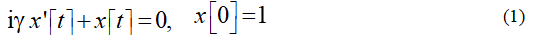
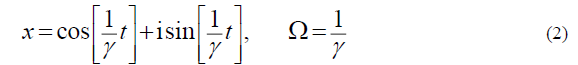
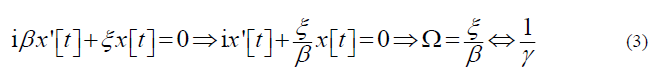
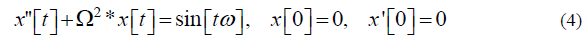
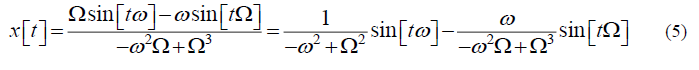
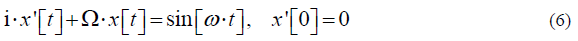
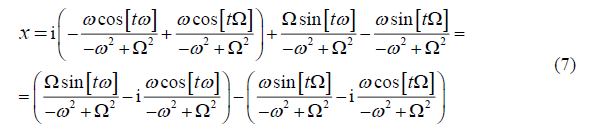
.jpg)