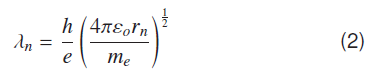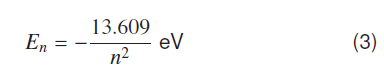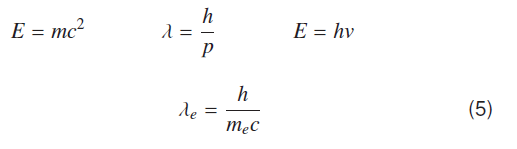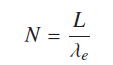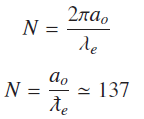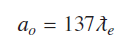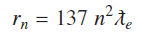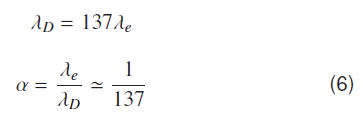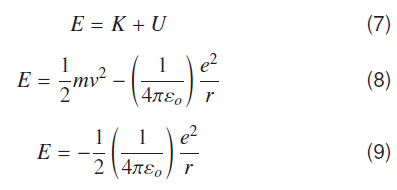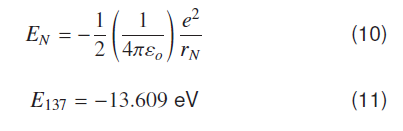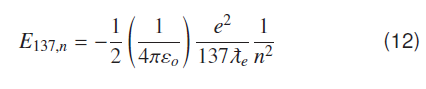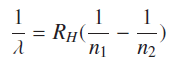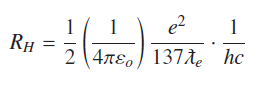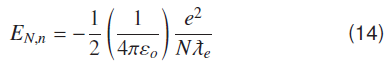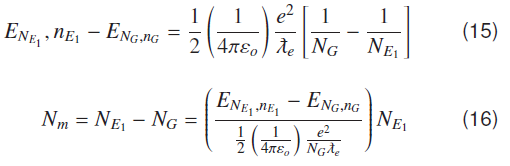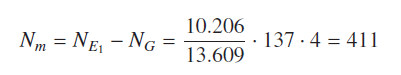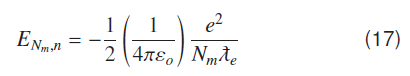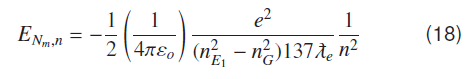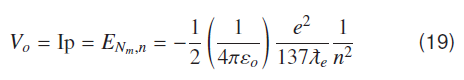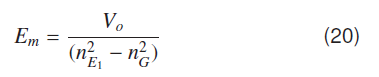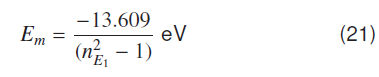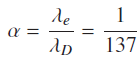Adjunct faculty, Physics and Astronomy at University of Waterloo, 200 University Avenue West, Waterloo, ON, Canada

*Corresponding Author: Asif Zaidi, Adjunct faculty, Physics and Astronomy at University of Waterloo, 200 University Avenue West, Waterloo, ON, Canada; Email: [email protected]

Received Date: February 3, 2023

Publication Date: March 30, 2023

Citation: Zaidi A. (2023). Atomic and Molecular Ground State Energy Estimation of  Hydrogen and Hydrogenic Molecules. Material Science. 5(2):18.

Copyright: Zaidi A. © (2023). 

ABSTRACT

This method enables one to calculate the binding energy of the ground state accurately for hydrogen molecule in a close form. Also, one can calculate the ground state binding energy of alkali metal homonuclear diatomic molecules. Ground state molecular energies can be calculated only by knowing the respective atomic ground and first excited state principle quantum numbers with their atomic ionization potential. This was possible by considering a bound electron as a vibrating string around a nucleus. The method exploits the Compton wavelength of an electron as a natural unit of length for atomic and molecular systems.

INTRODUCTION

It is well known that Bohr's orbital stability in hydrogen like or hydrogenic systems is explainable in terms of de Broglie waves in different allowed states like, 

However, to obtain orbital stability, one must calculate de Broglie wavelength 'λ_n' for nth radius considering Bohr's model

Equations (1) and (2) treat electron in nth orbit with radius like a standing wave. Where ‘n’ is analogous to Bohr's principal quantum number. This consideration predicts complete atomic energy levels, as nth radii is r_n =n²a₀ where a₀ = r_B = 0.529 x 10^-10 m is the Bohr's radius.

However, here we obtain all this by imposing a condition that we calculate de Broglie wavelength corresponding to Bohr's allowed orbits only [2]. In this paper this condition has been relaxed, because if bound electron behaves like a standing wave, then it is desirable that orbital stability condition should emerge more naturally. Orbital stability should be linked to some characteristic of orbiting particle like the length associated with the self-energy of electron i.e. the Compton wavelength of electron. As illustrated in following pages, use of Compton wavelength of electron has a clear advantage because with completion of atomic energy states, it also enables us to predict molecular ground states for hydrogenic systems.

Molecular ground state energy for hydrogen molecule has been discussed in many other papers with reference to Heitler London method [3], but solution is not a close form solution. Molecular hydrogen dissociation energy is also discussed by Konrad piszczatowski and coworkers as approximation as a power series of fine structure constant [4]. Also, thirteen terms approximation was done by James and Coolidge [5,6].

A recent paper has discussed reliability of fine structure constant of electromagnetic interactions around supermassive blackhole environment in a recent 2020 paper by A Hees. published in Physics review letters [7]. Accuracy of my results further supports reliability of modeling using fine structure constant α.

Representation of Atomic Energy Levels using Compton wavelength of Electron

According to Bohr’s model an electron in a potential field of proton such that it forms bound states,  atomic energy states can be represented as electron is in a potential well of depth -13.609eV [8].

n= 1,2,3,... represents ground and higher quantum states of this system.

This system can be visualized in another way i.e. bound states of electrons are stationary states. These stationary states exhibit similar properties as stationary waves on a string. A bound electron can be treated as a standing wave around proton with different possible states of string vibration i.e.

Wavelength corresponding to self energy of electron can be estimated using following well known equations due to A. Einstein, de Broglie and Max Plank, where symbols have their usual meanings.

Considering electronic orbits are stable and closed around a nucleus these orbits must contain Integral number of wavelengths “N” for orbital stability. If “L” is the path length and “λ” is the associated wave length then

Now considering the case of ground state of hydrogen atom number of waves in close orbit can be calculated using Bohr’s radius a₀

ƛ_e is electron Compton wavelength divided by 2π , and this with Bohr's radius a₀ of hydrogen gives number of waves in ground state to a very close approximation any little variation in exact value of N is due to uncertainty of measurements of constants involved.

Equation (5) represents Compton wavelength of electron [9], but when electron is bound to proton to form hydrogen atom, number of Compton wavelengths is 137 for ground state.

For any state of hydrogen atom nth Bohr’s state radius is given by using

λ_D is the deBroglie wavelength corresponding to the Bohr's first orbit. Since first Boher’s orbit contains one complete de Broglie wavelength. Atomic fine structure constant ‘α’ is given by.

Equation (6) is a very close approximation. Fine structure constant can be defined as is a ratio of electron Compton wave length and de Broglie wavelength in a given atomic orbit.

Atomic Energy Levels for Hydrogenic Systems

For the bound state, energy conservation in hydrogenic systems is given by;

Dynamical Energy changes with number of Compton waves ‘N’ in different orbits.

As above equation (10) indicates when number of Compton waves are ‘137’ around a proton in the ground state of hydrogen atom, electron is bound to proton with binding energy of −13.609 eV. This is the ionization energy of hydrogen atom in the ground state. Energy values of all other states can be found by considering that out of ‘N’ possible vibrating states some states are allowed states. A bound state occurs whenever number of Compton waves divided by 137 is a whole number. Comparing ′r_N′ and Bohr’s nth radius ′rn′ gives relation between Bohr’s principal quantum number ‘n’ and ‘N’, N=137 n² r_N and  = N ƛe. Hydrogenic states can conveniently be represented as quantized form of coulomb potential, if electron Compton wavelength is used a natural unit length for atomic and molecular systems.

n = 1,2,3,...

This formula (12) generates all observed atomic energy states of hydrogen atom i.e. over hydrogenic scale 137 is a constant scaling factor for atomic systems in coulomb field.

Using equation (12) Rydberg formula for hydronic states can be calculated as.

n₂ > n₁, where “n” is Bohr’s principle quantum number. 

And Rydberg constant

Symbols have usual meanings; calculated value of Rydberg constant is R_H = 1.097×107m⁻¹. Entire Hydrogen atomic spectrum can be generated by above Rydberg’s formula.

Molecular Ground State Energy for hydrogen like molecules

Use of Compton wavelength of electron can be extended to find bound state energy of hydrogen molecule. When individual atoms are at appropriate distance to form a molecule, their electrons form stationary waves over two protons. Number of waves ‘N’ should enlarge accordingly like N_molecule > N_atomic for a molecular ground state; but this number of waves should be less than first atomic excited state. A molecular energy ground state has ′N_m′ number of wavelengths that can be found as;

Number of waves for first excited atomic state; N_G = Number of waves for ground state.

In Coulomb potential A molecular or atomic bound state occurs whenever number of waves in a possible molecular or atomic orbit divided by 137 is a whole number. This can be regarded as law of Coulombic bound states. To estimate number of Compton waves in a hydrogen like molecular ground state, considering equation (12) for atomic energy levels for a given "n"

For ground and first excited state of hydrogen atom, N, n →N_G, n_G and  respectively

 

where and ,n_G = -13.609 eV and  , = −-3.4022 eV, using this in equation (16) gives,

Since 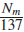 this indicates that the bound molecular ground state of hydrogen molecule contains three complete deBroglie waves. Hence energy value corresponding to 411 Compton waves should be a bound state in Coulomb potential for the same reason as established for the stability of hydrogen atom. Molecular ground state can also be calculated by the formula for hydrogen molecule and similar systems by considering general energy formula for hydrogen like atomic systems with ‘N’ Compton waves.

Using Equation (14) for molecular ground state energy.

Using (13) and (17) results

n = 1,2,3,...

Equation (18) represents energy of a hydrogenic molecular system corresponding to the nth atomic ground state where V₀ or IP is the depth of the atomic potential well (or atomic ionization potential) as seen by valence electron.

Molecular ground state energy E_m for hydrogenic systems can be expressed as;

where n_G and  are Bohr's quantum numbers for ground and first excited atomic states. Molecular ground state energy for the hydrogen molecule is given by using atomic ionization potential V₀ = -13.609 eV and the ground state n_G = 1

Formula (20) is a close form solution, this gives excellent result for the ground state of hydrogen like molecules, but molecule energy values E_m in general will depend on values of atomic potential well depth V₀ obtained from equation (19). Equation (19) does not include screening due to inner shell electrons, however if experimental value for V₀ is taken i.e., atomic ionization potential and used with formula (20) results for Alkali metal molecules are also good as well. The following table compares values calculated by equation (20) and experimentally observed molecular ground state energy.

Considering first example to calculate numerically value of simplest hydrogen molecule, derived formula for ionization potential (19) gives ionization potential of -13.609 eV and derived formula (20) yields molecular ground state energy of – 4.536 eV, by using ground state quantum number n_G = 1 and excited state quantum number   = 2. This is a calculation in a close form without any approximation. As a second example considering larger sodium molecule Na₂. In this calculation atomic ionization potential V₀ = 5.14, ground state quantum number n₁ = 3;   = 4. Using equation (20) yields molecular ground state energy of Na₂ molecule as – 0.73 eV. This is very close to accepted value for sodium molecule given in column 3 of Table1. This has percentage error of only 1.39%. Table 1 second column contains theoretically calculated values by using derived formulas (19) and (20). Third column lists accepted values of molecular ground state binding energies.

Table1: Comparison of Molecular ground state energy calculation for hydrogenic molecules of first group with experiment (Accepted value).

Molecule (1st Group)	Molecular Energy Em (eV) (Calculated)	Molecular Energy Em (eV) (Accepted)	% Error
H2	- 4.536	- 4.556	0.44
Li2	- 1.078	-1.046	3.06
Na2	- 0.730	- 0.720	1.39
K2	- 0.482	- 0.514	6.22
Rb2	- 0.389	- 0.490	20.61
Cs2	- 0.299	- 0.394	24.11

CONCLUSIONS

Relation obtained among molecular ground state energy and well depth (ionization energy of atomic ground state) shows that, such a relation is clearly visible if Compton wavelength of electron is used as a unit of length for atomic and molecular systems instead of Bohr's radius. This indicates that Compton wavelength of electron is a natural unit of length for the scale of atomic and molecular systems.

This method predicts near exact values for the molecular ground states where system has no valence electron screening effect. Deviation from experiment for Rubidium and Cesium is due to large screening of valence electron and relatively small well depth.

It appears that bound electron around proton can be treated as a vibrating string.

As equation (6) indicates the value of fine structure constant ′α′ emerges naturally as a ratio of electron Compton wavelength and de Broglie wavelength of electron in the same orbit.

ACKNOWLEDGEMENTS

I wish to thank professors Kuhrsheed Siddiqi and Dr. Iqbal for discussing this subject in detail and  their useful suggestions.

REFERENCES

1. Bohr N. (1913). Phil Mag. 26(1):26.
2. de Broglie L. (1924). Phil Mag. 47:446
3. Heitler W, London F. (1927). Wechselwirkung neutraler Atome und homöopolare Bindungnach der Quantenmechanik. Zeitschrift fur Physik, 44:455-472.
4. Piszczatowski K, Łach G, Przybytek M, Komasa J, Pachucki K, Jeziorski B. (2009). Theoretical Determination of the Dissociation Energy of Molecular Hydrogen. J Chem Theory Comput. 11:3039-3048
5. James HM, Coolidge AS. (1933).The Ground State of the Hydrogen Molecule. A S J Chem Phys. 1:825.
6. James HM, Coolidge AS. (1935). Explicitly Correlated Electrons in Molecules .A S J Chem Phys. 3:129.
7. Hees A, Do T, Roberts BM, Ghez AM, Nishiyama S, Bentley RO, et al. (2020). Search for a Variation of the Fine Structure Constant around the Supermassive Black Hole in Our Galactic Center. Phys Rev Lett. 124:081101.
8. Bransden BH, Joachain CJ. (2003). Physics of atoms and molecules. Prentice Hall, England, Quantum Mechanics.
9. Compton AH. (1923). The Spectrum of Scattered X-Rays. Phys Rev. 22:409